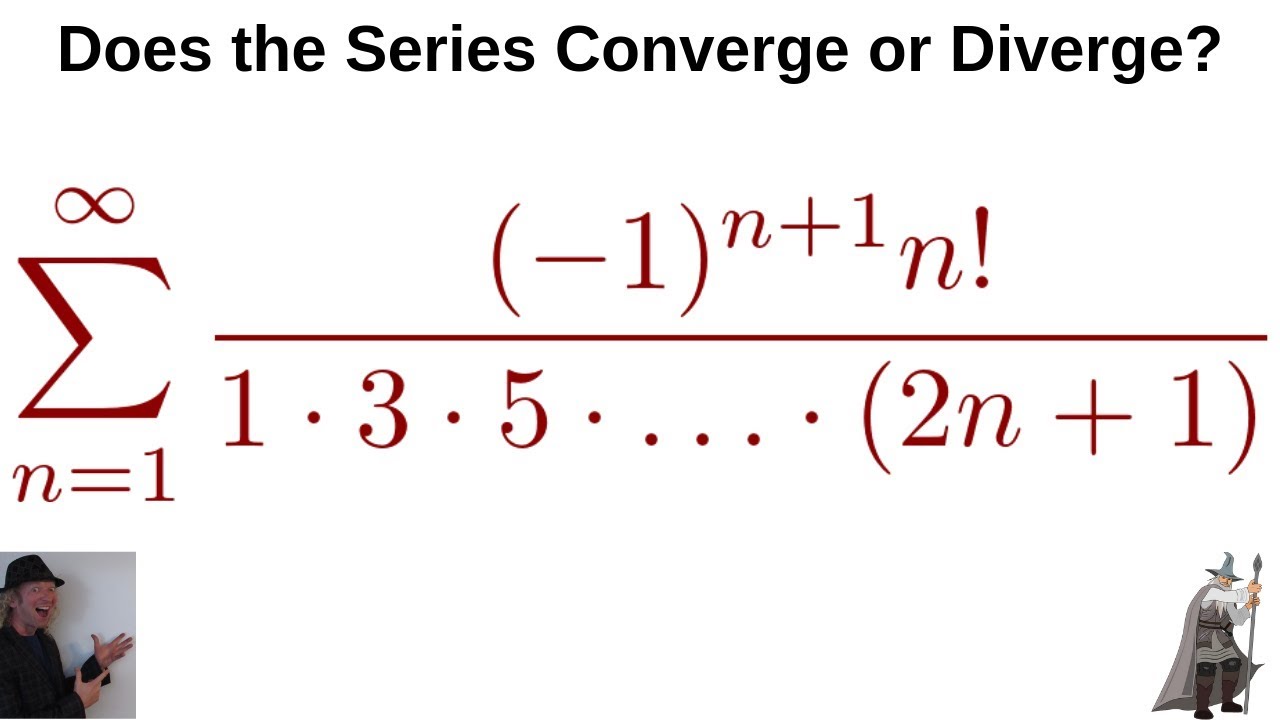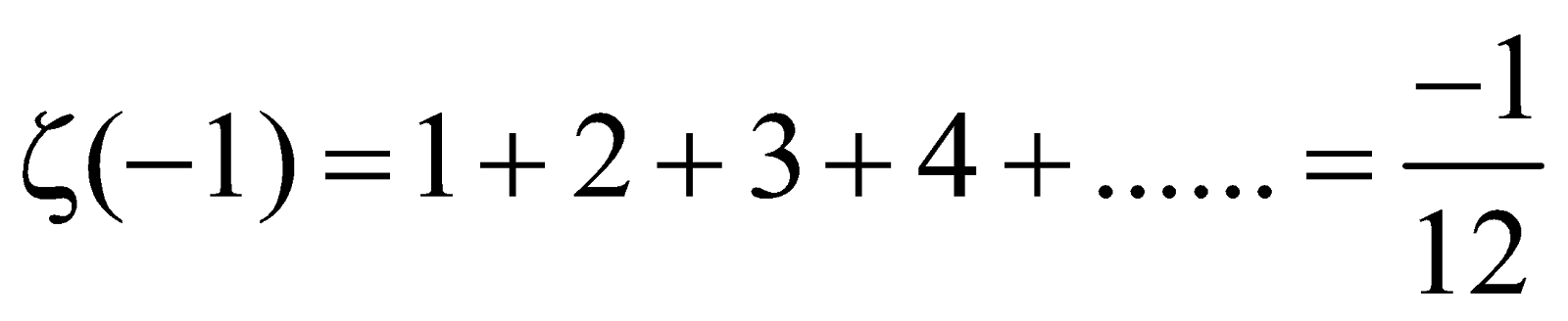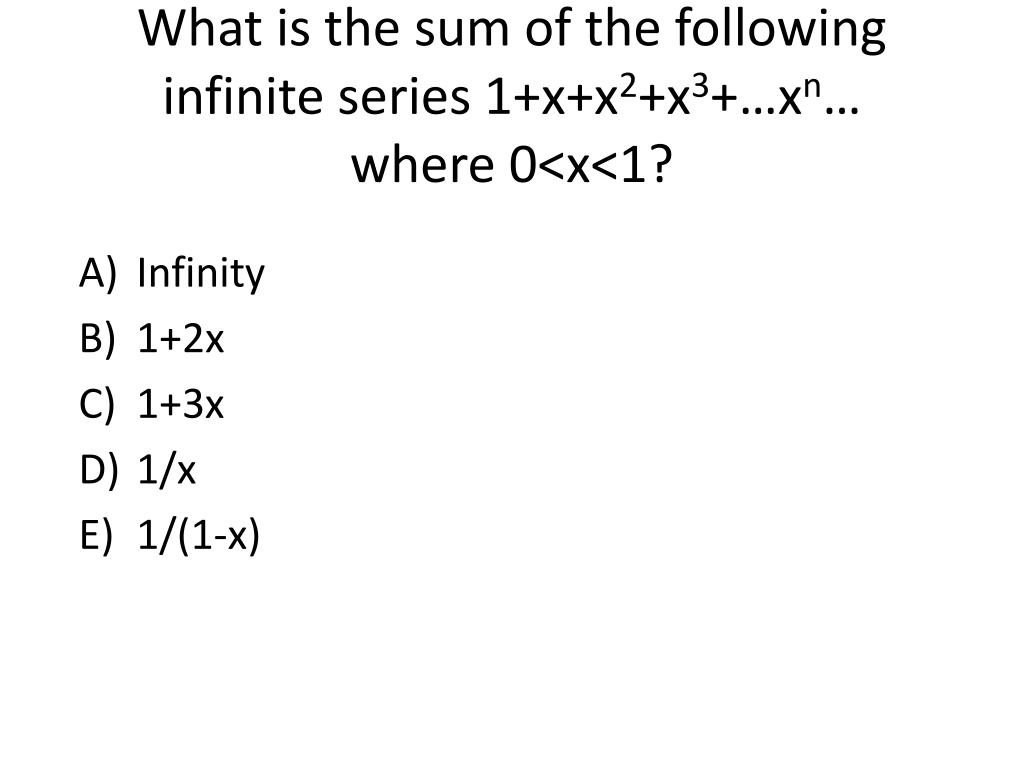1 1 1 1 1 1 Infinite Series

Infinite series 415 n 1 5 10 20 2 3 n 0 6667 0 1316872428 0 01734152992 0 00030072866 we observe that as n becomes larger and larger 2 3 n becomes closer and closer to zero.

1 1 1 1 1 1 infinite series. 12 14 18 116. We get an infinite series. How is this possible. We therefore need a precise definition of an infinite sum and having defined this concept we must verify whether the laws established for finite sums are valid for.

We ll start with a sequence left a n right n 1 infty and again note that we re starting the sequence at n 1 only for the sake of convenience and it can in fact be anything. Find the value of 51 2 51 4 51 8. When we have an infinite sequence of values. More links stuff in full description below a little bit of.

A different result is obtained when we group the terms as follows. Discussing the brain bending grandi s series and thomson s lamp featuring dr james grime. How it is. In mathematics the infinite series 1 1 1 1 also written is sometimes called grandi s series after italian mathematician philosopher and priest guido grandi who gave a memorable treatment of the series in 1703 it is a divergent series meaning that it lacks a sum in the usual sense on the other hand its cesàro sum is 1 2.

This particular series is relatively harmless and its value is precisely 1. Is 23 and the sum of squares of infinite. 12 14 18 116. The sum of an infinite g.

Viewed 11 times 0 begingroup in the records its sum is given as dfrac 1 2. Even if we go till infinity answer can either be 0 or 1. The sum of infinite terms that follow a rule. The more terms the closer the partial sum is to 1.

Regarding sum of infinite series 1 1 1 1 1 1 cdots cdots ask question asked today. To see why this should be so consider the partial sums formed by stopping after a finite number of terms. Similar paradoxes occur in the manipulation of infinite series such as 1 2 1 4 1 8 1 continuing forever. And group its terms in succession by twos we obtain 1 1 l l 0.

Which follow a rule in this case each term is half the previous one and we add them all up. In an infinite gp series the first term is p and infinite sum is s then p.